更新历史

2023-07-20

发布博客

前言

前置芝士

线性 dp

斜率优化模板

思路

若有一维的 dp 方程形如

$\large F(i)=\min_{j\in[0,i)}\{f(j)-a_i\times d_j\}$

其中 $f(j)$ 必须包含 $dp_j$ 且只与 $j$ 有关， $F(i)$ 必须包含 $dp_i$ 且只与 $i$ 有关

且满足

$\large a_j\le a_i,d_j\le d_i(j<i)$

则暴力算需要 $O(n^2)$ 的时间复杂度。而且不能直接用单调队列优化，因为它有一个既包含 $i$ 又包含 $j$ 的项 $a_i\times d_j$ 。

遇到这种方程，就可以用斜率优化来求解。

考虑如何求出 $F(i)$ 的值。

我们将原方程作一些换元

$\large b=F(i),y_j=f(j),k=a_i,x_j=d_j$

则原方程变为了

$\large b=\min_{j\in[0,i)}\{y_j-k\times x_j\}$

其中 $k$ 和 $x$ 是单调递增的。

再令 $b_j=y_j-k\times x_j$ ，则 $F(i)=b=\min_{j\in[0,i)}b_j$ 。

观察 $b_j$ 的表达式，可以发现 $b_j$ 刚好是「斜率为 $k$ 且过 $(x_j,y_j)$ 的直线」的截距。

也就是说，如果我们能用 $O(1)$ 的时间算出最小的截距对应的 $j$ ，就能做到 $O(1)$ 转移，总体复杂度也就是 $O(n)$ 了。

那么我们把所有 $j$ 对应的点 $P_j(x_j,y_j)$ 描出来，如下图就是一种 $i=5$ 时的情况：

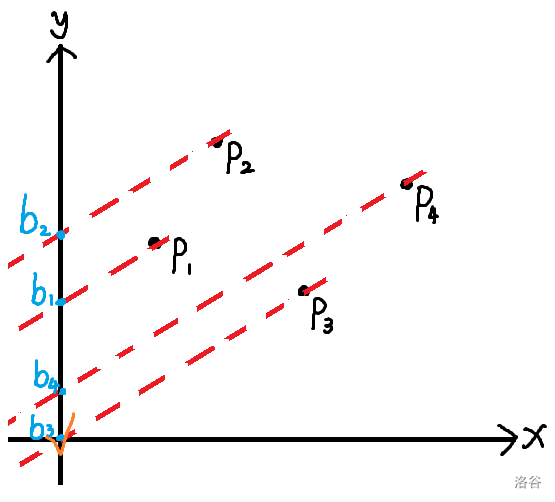
注意，由于 $x$ 的单调递增，每个点是从左往右排的。

容易发现，将一条斜率为 $k$ 的直线从下往上平移，直至碰到其中一个点，这时这条直线的截距 $b$ 最小，碰到的点的编号就是最佳转移的 $j$ 值。比如上图中的最佳转移的 $j$ 值就为 $3$ 。

而显然，第一个碰到的点一定在这 $i-1$ 个点构成的下凸壳上，所以我们不需要枚举前面所有的 $(x,y)$ ，而只需要枚举在下凸壳上的 $(x,y)$ 即可。

但是面对极端数据，这样的做法还是会达到 $O(n^2)$ 的时间复杂度，怎么办呢？

我们发现上面还有一个斜率 $k$ 单调递增的条件没有用上。

加上这个条件，我们发现这个碰到的点除了会在下凸壳上，而且它的编号还是单调不减的 ~~（感性理解一下）~~ 。

那就好办了。每次找到下凸壳上会碰到的点后，将这个点之前的点全部从下凸壳删除，就可以保持总体 $O(n)$ 的时间复杂度（每个点最多被查询一次，就会被删除）。

接下来就是一些实现的写法，由于用到了斜率来维护所以叫斜率优化。

下面的说明中， $K(p1,p2)$ 代表第 $p1$ 和 $p2$ 个点所连成的直线的斜率。

$X(p)$ 指上文提到的第 $p$ 个点所对的 $x=d_i$ ， $Y(p)$ 同理。

一：如何查找下凸壳上第一个碰到的点，并删除之前的点

假设现在已经有的下凸壳是由，下标为 $q_l$ 至 $q_r$ 的点构成的（实际上就是一个单调队列，维护的是相邻2个点间的斜率递增），那么算出下标 $i$ 对应的 $k_i$ 。

在 $q$ 中还有至少2个点时，比较 $K(q_l,q_{l+1})$ 与 $k_i$ 的大小关系。若前者较小，则弹出队首 l++。否则对应的 $l$ 就是我们要找的那个点。

代码如下：

double K(int p1,int p2){
    int x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2);
    return (y2-y)*1.0/(x2-x);
}
while(l<r&&K(q[l],q[l+1])<k[i]) l++;
//注意是l<r而不是l<=r
int j=q[l];

当然，开始时要存入一个编号为 $0$ 的点，也就是固定值 $dp_0$ 。

q[++r]=0;

为了避免精度问题，也可以用乘法来比较斜率：

bool cmp1(int p1,int p2,int kk){
    int x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2);
    return (y2-y)<kk*(x2-x);
}
while(l<r&&cmp1(q[l],q[l+1],k[i])) l++;
//注意是l<r而不是l<=r
int j=q[l];

二：如何维护下凸壳

我们在通过上面算出最佳的 $j$ 后，就可以对 $dp_i$ 进行转移。转移完以后，就可以算出对应的点 $P_i(x,y)$ 。

在 $q$ 中还有至少2个点时，比较 $K(q_{r-1},q_r)$ 和 $K(q_r,i)$ 的大小。若前者较大，则弹出队尾 r--。否则退出循环，将第 $i$ 个点加入下凸壳 q[++r]=i。

代码如下：

double K(int p1,int p2){
    int x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2);
    return (y2-y)*1.0/(x2-x);
}
while(l<r&&K(q[r-1],q[r])>K(q[r],i)) r--;
//注意是l<r而不是l<=r
q[++r]=i;

改成乘法如下：

bool cmp2(int p1,int p2,int p3){
    int x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2),x3=X(p3),y3=Y(p3);
    return (y2-y)*(x3-x2)>(y3-y2)*(x2-x);
}
while(l<r&&cmp2(q[r-1],q[r],i)) r--;
//注意是l<r而不是l<=r
q[++r]=i;

模板例题

例题：P3628 特别行动队

洛谷传送门

给定一个长度为 $n$ 的序列 $x$ ，以及一个二次函数 $F(X)=A\cdot X^2+B\cdot X+C$ 。要求将序列分成若干段连续区间，一段区间 $[l,r]$ 的权值为 $F(\sum\limits_{i=l}^r x_i)$ ，求最大权值和。

解题思路

这题是一道斜率优化模板题。

首先列出原始的 dp 方程：

$\large dp_i=\max_{j\in[0,i)}\{dp_j+A\times(sum_i-sum_j)^2+B\times(sum_i-sum_j)+C\}$

其中 $sum$ 表示 $x$ 的前缀和。

化简之后得到：

$\large dp_i=\max_{j\in[0,i)}\{dp_j+A\times sum_i^2-2A\times sum_isum_j+A\times sum_j^2+B\times sum_i-B\times sum_j+C\}$

$\large dp_i-A\times sum_i^2-B\times sum_i-C=\max_{j\in[0,i)}\{dp_j+A\times sum_j^2-B\times sum_j-2A\times sum_isum_j\}$

这时候， $y$ ， $k$ ， $x$ ， $b$ 的取值就能确定了：

$\large y=f(j)=dp_j+A\times sum_j^2-B\times sum_j$

$\large k=a_i=2A\times sum_i$

$\large x=d_j=sum_j$

$\large b=dp_i-A\times sum_i^2-B\times sum_i-C$

$b$ 的取值虽然也确定了，但是程序中用不到，写出来就是为了好理解一些。

然后就用上面的板子套就行了。

唯一要注意的是，此题求的是最大值，所以需要将维护下凸壳改为维护上凸壳。具体方法是把两个 cmp 函数里判断大小的符号改一下即可。

参考代码

#include <bits/stdc++.h>
using namespace std;
//不开long long见祖宗
typedef long long ll;
ll n,a,b,c,s[1000005],dp[1000005],q[1000005],l=1,r=0;
ll Y(ll x){return dp[x]+a*s[x]*s[x]-b*s[x];}
ll K(ll x){return 2*a*s[x];}
ll X(ll x){return s[x];}
bool cmp1(ll p1,ll p2,ll kk){
    ll x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2);
    return (y2-y)>kk*(x2-x);//此处'<'改为'>'
}
bool cmp2(ll p1,ll p2,ll p3){
    ll x=X(p1),y=Y(p1),x2=X(p2),y2=Y(p2),x3=X(p3),y3=Y(p3);
    return (y2-y)*(x3-x2)<(y3-y2)*(x2-x);//此处'>'改为'<'
}
int main(){
    scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
    q[++r]=0;
    for(ll i=1;i<=n;i++) scanf("%lld",&s[i]),s[i]+=s[i-1];
    for(ll i=1;i<=n;i++){
        while(l<r&&cmp1(q[l],q[l+1],K(i))) l++;
        ll j=q[l];
        dp[i]=dp[j]+a*(s[i]-s[j])*(s[i]-s[j])+b*(s[i]-s[j])+c;
        //通过最初的dp方程转移会清晰一点
        while(l<r&&cmp2(q[r-1],q[r],i)) r--;
        q[++r]=i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}