回文树（PAM）的学习笔记

更新历史

更新历史

2023-08-18

发布博客

前言

前置芝士

字典树

---

一些约定

• 文中所有的字符串下标均从 $1$ 开始。

• 文中的 $i,j$ 下标，如无特殊说明，分别指「字符串的下标」和「回文树节点的下标」，$S_i$ 表示字符串 $S$ 的第 $i$ 个字符，$tr_j$ 表示回文树的第 $j$ 个节点。

---

定义

回文树跟字典树一样，都是用树形结构存储一些字符串，但字典树存储的是若干毫不相干的字符串，而回文自动机存储的是一个字符串中，所有的回文子串。

那么我们考虑回文树的存储方式。

回文树中存储的都是回文串，那么很容易想到将回文串折半进行存储。

但这样有个小问题，就是奇偶长度回文串的折半方式并不一样。既然一颗树存储不了，那就开两棵树啊。

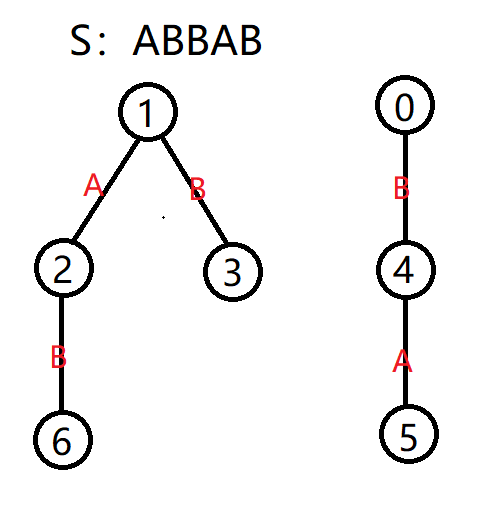
如上图：

• 设以 $1$ 号点为根的树是奇数长度回文串的树，则节点 $2,3,6$ 分别对应子串 $\texttt{A,B,BAB}$。

• 设以 $0$ 号点为根的树是偶数长度回文串的树，则节点 $4,5$ 分别对应子串 $\texttt{BB,ABBA}$。

这些回文串刚好对应了原串 $S$ 的所有回文子串：$\texttt{A,B,BB,ABBA,BAB}$（相同的回文子串只算一次）。

从这个例子中还可以发现，设 $tr_j$ 是 $tr_j$ 父亲的 $x$ 字符子节点，则 $tr_j$ 所对应的字符串，总是在 $tr_j$ 父亲所对应的字符串两边同时添加一个 $x$ 字符所得到。

如图中的 $tr_6$ 是 $tr_2$ 的 $\texttt{B}$ 类子节点，则 $tr_6$ 所对应的字符串 $\texttt{ABA}$ 就是在 $tr_2$ 所对应的字符串 $\texttt{A}$ 两边同时添加一个 $B$ 字符所得到。

接下来就要尝试构造这两棵树。

---

构造

插入

首先证明一个 不那么 显然的引理：

每在字符串末尾增加一个字母，回文子串的数量至多会增加 $1$。

证明很简单，可以使用反证法。

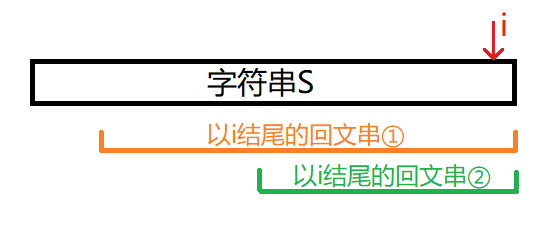
设增加的字母为 $S_i$，且以 $S_i$ 为结尾的新增回文子串至少有两个。

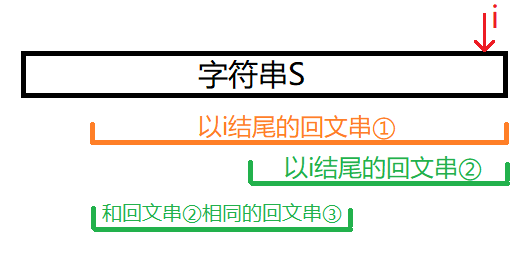
那么根据回文串的性质，「回文串2」在通过「回文串1」中线对称后的「回文串3」和「回文串2」完全相同，也就是说「回文串2」在插入 $S_i$ 之前就已经存在了。

也就是说，我们可以每次在原字符串末尾增加一个字符，再进行更新回文树。

假设我们现在在插入 $S_i$，容易发现，在以 $i$ 为结尾的每一个回文串中，只有最长的那个才有可能成为新增回文串。

显然，这个「以 $i$ 结尾的最长回文串」是在「以 $i-1$ 结尾的某个回文串」的两边各增加一个相同的字符得到的（图中红色线段为相同字符）。即，我们需要找到「以 $i-1$ 结尾的最长回文串」满足这个回文串的左右两个字符是相同的，我们暂且将这种字符串称为“可拓展的”。

而「以 $i-1$ 结尾的某个回文串」一定已经在回文树上存储过，那么我们只需在这个「以 $i-1$ 结尾的某个回文串」所对应的节点下新增一个 $S_i$ 节点即可。

接下来的目标，就是找到要往哪个节点下增加一个子节点。

---

由于回文树的每个节点都对应一个回文串，所以我们可以为 $tr_j$ 确定一个长度，用 $len_j$ 来保存。容易发现，树上每个节点的 $len$ 值，都等于其父亲节点 $len$ 值增加 $2$。为了方便，对于点 $0,1$ 的 $len$ 值，我们分别设置成 $0,-1$。

假设我们现在在插入 $S_i$，那么假设以第 $i-1$ 个点结尾的每一个回文串中最长的那个，所对应在回文树上的节点为 $last$。特别地，一开始 $last$ 的值设为 $1$。

如果我们运气特别好，${S_{i-len_{last}-1}}$ 恰好等于 ${S_i}$，则「以 $i-1$ 结尾的最长回文串」就是可拓展的，那么我们显然可以直接将 $S_i$ 加在 $tr_{last}$ 下面。

举个栗子：假如我们要插入 $S=\texttt{ABBAB}$ 中的第 $4$ 个字符 $\texttt{A}$，那么我们已经建好了 $S$ 前 $3$ 个字符构成的回文树。

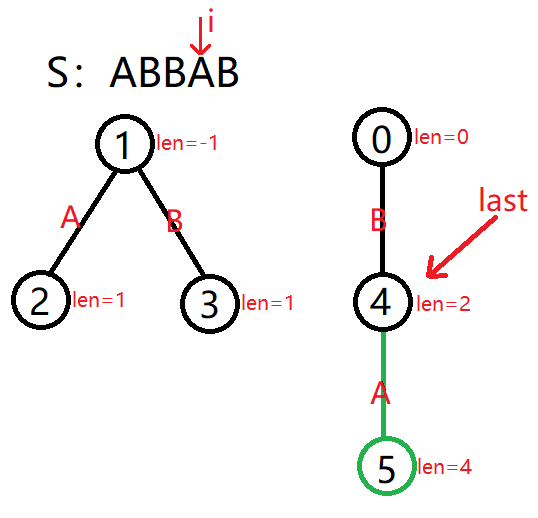
此时要插入的 $S_i=S_4$，以 $S_{i-1}=S_3$ 为结尾的「最长回文子串」是 $\texttt{BB}$，长度 $len=2$，所以 $last=4$。

可以发现，${S_{i-len_{last}-1}=S_{4-2-1}=S_1=\texttt{A}=S_i}$，也就是说 $\texttt{BB}$ 这个回文子串是可拓展的，所以我们就可以在 $\texttt{BB}$ 的两边各增加一个 $\texttt{A}$ 字符，变成 $\texttt{ABBA}$，即为以 $S_i$ 为结尾的「最长回文子串」，那么就可以把 $S_i=\texttt{A}$ 直接加在 $tr_{last}$ 下面。

---

但在大部分情况中，这个式子是不成立的。这个式子本质是：在以 $S_{i-1}$ 为结尾的「最长回文子串」两边拓展一个字符，此时「最长的回文子串」拓展不了，自然而然地，就会想到用「第二长的回文子串」。若「第二长的子串」还是拓展不了，就用「第三长的」，以此类推。

容易发现,「第二长的回文子串」即为「最长回文子串」的最长回文后缀，而「第三长的回文串」即为「第二长的回文子串」的最长回文后缀，依次类推。

也就是说，我们只要记录每个回文串的「最长回文后缀」，如果当前子串不能拓展，就通过“跳跃”到其最长回文后缀，来找到最长的能拓展的回文子串。我们把这个过程叫做后缀链跳跃。

我们在每个节点 $j$ 上记录一个指针 $fail_j$，指向其代表的回文串的「最长回文后缀」在回文树上对应的节点。特别地，规定 $fail_0=1,fail_1=0$。

再举个栗子：假如我们要插入 $S=\texttt{ABBAB}$ 中的第 $5$ 个字符 $\texttt{B}$，那么我们已经建好了 $S$ 前 $4$ 个字符构成的回文树。

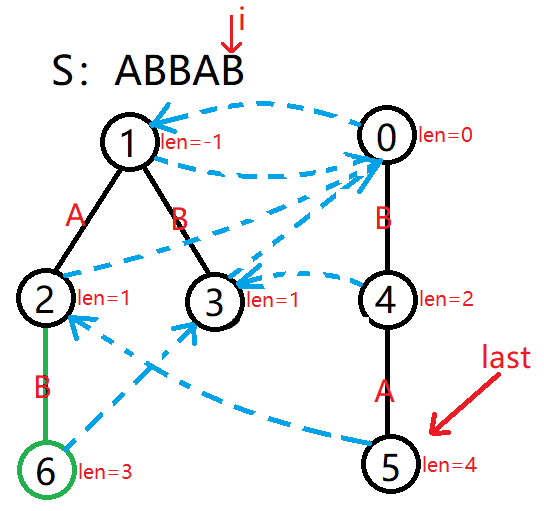
此时要插入的 $S_i=S_5$，以 $S_{i-1}=S_4$ 为结尾的「最长回文子串」是 $\texttt{ABBA}$，长度 $len=4$，所以 $last=5$。

此时，${S_{i-len_{last}-1}=S_{5-4-1}=S_0=\varnothing \neq S_i}$，则「以 $i-1$ 结尾的最长回文串」不可拓展，所以考虑用以 $S_4$ 结尾的「第二长回文子串」，即「最长回文子串」 $\texttt{ABBA}$ 的最长回文后缀，也就是 $fail_{last}=fail_5$ 指向的 $tr_2$ 所对应的字符串 $\texttt{A}$，它的 $len=1$。

我们检查能否在回文串 $\texttt{A}$ 两边进行一次拓展，即判断 ${S_{5-len_2-1}=S_{5-1-1}=S_3=\texttt{A}=S_i}$，可以拓展，我们就可以在 $tr_2$ 的下面新建一个节点。

---

fail 指针

现在还有最后一个问题，就是插入节点后，如何计算其的 $fail$ 指针。

这个过程和找可以拓展的「最长回文后缀」是非常相近的，只不过找「最长回文后缀」时，是从 $tr_{last}$ 开始后缀链跳跃，而找 $tr_j$ 的 $fail$ 指针时，是从 $fail_{fa(tr_j)}$ 开始进行后缀链跳跃。

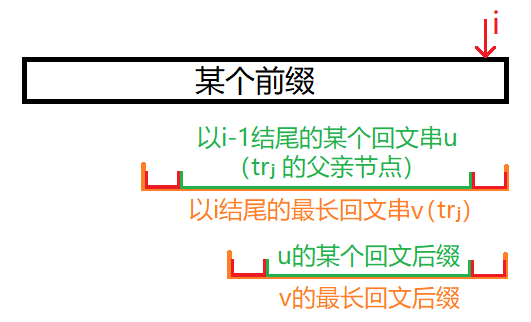
如图，我们要找的就是「$v$ 的最长回文后缀」，而「$v$ 的最长回文后缀」就是又「$u$ 的某个回文后缀」的两边加上两个一样的字符得到的。

那么这个「$u$ 的某个回文后缀」就是 $u$ 的最长可拓展后缀，其求法和之前插入节点的做法完全相同。

虽然 $u$ 所对应的节点就是 $tr_j$ 的父亲节点，但由于「$u$ 的某个回文后缀」是严格的后缀，所以不能直接从 $tr_j$ 的父亲节点开始跳，而是要从 $fail_{fa(tr_j)}$ 开始跳，否则得到的可拓展后缀就不是严格的了。

值得注意的是，若 $tr_j$ 的父亲节点是 $1$ 号节点，则 $tr_j$ 所对应的回文串只有一个字符，那么就令 $tr_j$ 的 $fail$ 指针指向 $0$ 号节点，毕竟空串是所有字符串的后缀。

---

构造过程模拟

最后，让我们把插入 $S=\texttt{ABBAB}$ 的全过程模拟一遍。

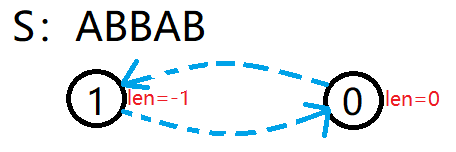
• 初始状态：只有 $tr_1$ 和 $tr_0$，$len$ 值分别为 $-1$ 和 $0$，$fail$ 指针分别指向 $0$ 和 $1$。

---

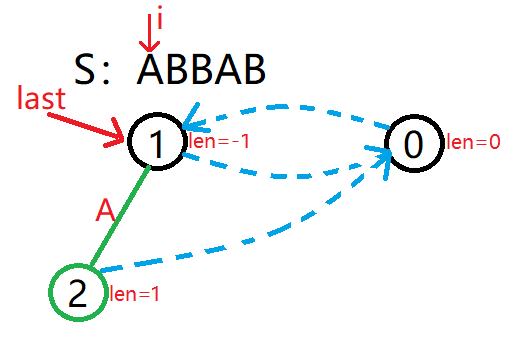
• 插入 $S=\texttt{ABBAB}$ 中的第 $1$ 个字符 $\texttt{A}$，并且此时 $last$ 指向 $1$。

• 由于 ${S_{i-len_1-1}=S_{1-(-1)-1}=S_1=\texttt{A}=S_1=S_i}$，所以直接在 $tr_1$ 下面新建一个 $\texttt{A}$ 节点（$tr_2$）即可，节点所对的回文串的 $len$ 值为 $(-1)+2=1$。

• 进行此节点 $fail$ 指针的计算：$tr_2$ 的父亲节点是 $tr_1$，则直接将 $fail_2$ 指向 $0$ 号节点。

• 最后更新 $last$ 指针指向 $2$。

---

• 插入 $S=\texttt{ABBAB}$ 中的第 $2$ 个字符 $\texttt{B}$，那么我们已经建好了 $S$ 前 $1$ 个字符构成的回文树，并且此时 $last$ 指向 $2$。

• 此时 ${S_{i-len_2-1}=S_{2-1-1}=S_0=\varnothing \neq S_2=S_i}$，所以接着判断 $fail_2$ 指向的 $tr_0$。
  此时 ${S_{2-len_0-1}=S_{2-0-1}=S_1=\texttt{A} \neq S_2=S_i}$，所以接着判断 $fail_0$ 指向的 $tr_1$。
  由于 ${S_{2-len_1-1}=S_{2-(-1)-1}=S_2=\texttt{B}=S_2=S_i}$，所以在 $tr_1$ 下面新建一个 $\texttt{B}$ 节点（$tr_3$）即可，节点所对的回文串的 $len$ 值为 $(-1)+2=1$。

• 进行此节点 $fail$ 指针的计算：$tr_3$ 的父亲节点是 $tr_1$，则直接将 $fail_3$ 指向 $0$ 号节点。

• 最后更新 $last$ 指针指向 $3$。

---

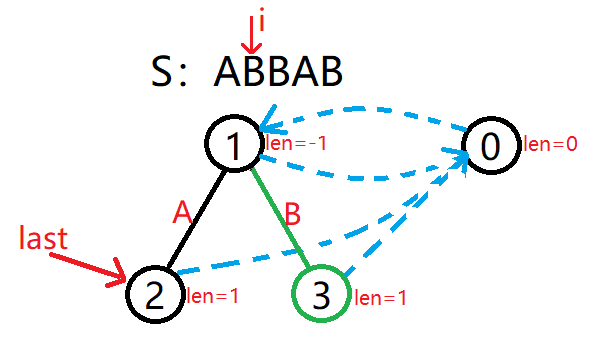
• 插入 $S=\texttt{ABBAB}$ 中的第 $3$ 个字符 $\texttt{B}$，那么我们已经建好了 $S$ 前 $2$ 个字符构成的回文树，并且此时 $last$ 指向 $3$。

• 此时 ${S_{i-len_3-1}=S_{3-1-1}=S_1=\texttt{A} \neq S_3=S_i}$，所以接着判断 $fail_3$ 指向的 $tr_0$。
  由于 ${S_{i-len_0-1}=S_{3-0-1}=S_2=\texttt{B}=S_3=S_i}$，所以在 $tr_0$ 下面新建一个 $\texttt{B}$ 节点（$tr_4$）即可，节点所对的回文串的 $len$ 值为 $0+2=2$。

• 进行此节点 $fail$ 指针的计算：$tr_4$ 的父亲节点是 $tr_0$，所以从 $fail_0$ 指向的 $tr_1$ 开始判断。
  由于 $S_{3-len_1-1}=S_{3-(-1)-1}=S_3=\texttt{B}=S_3=S_i$，匹配成功，所以将 $fail_4$ 指向 $tr_1$ 的 $\texttt{B}$ 儿子 $3$ 号节点。

• 最后更新 $last$ 指针指向 $4$。

---

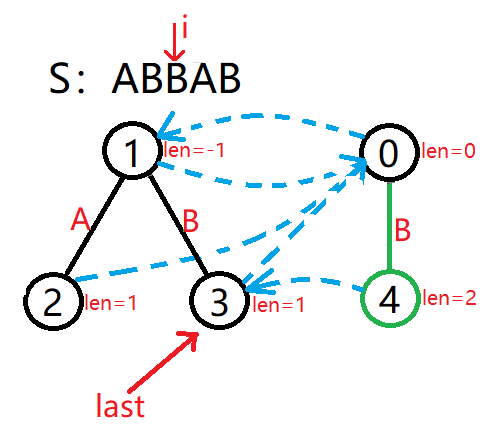
• 插入 $S=\texttt{ABBAB}$ 中的第 $4$ 个字符 $\texttt{A}$，那么我们已经建好了 $S$ 前 $3$ 个字符构成的回文树，并且此时 $last$ 指向 $4$。

• 由于 ${S_{i-len_4-1}=S_{4-2-1}=S_1=\texttt{A}=S_4=S_i}$，所以直接在 $4$ 号节点下面新建一个 $\texttt{A}$ 节点（$tr_5$）即可，节点所对的回文串的 $len$ 值为 $2+2=4$。

• 进行此节点 $fail$ 指针的计算：$tr_5$ 的父亲节点是 $tr_4$，所以从 $fail_4$ 指向的 $tr_3$ 开始判断。
  此时 ${S_{4-len_3-1}=S_{4-1-1}=S_2=\texttt{B} \neq S_4=S_i}$，所以接着判断 $fail_3$ 指向的 $tr_0$。
  此时 ${S_{4-len_0-1}=S_{4-0-1}=S_3=\texttt{B} \neq S_4=S_i}$，所以接着判断 $fail_0$ 指向的 $tr_1$。
  由于 ${S_{4-len_1-1}=S_{4-(-1)-1}=S_4=\texttt{A}=S_4=S_i}$，匹配成功，所以将 $fail_5$ 指向 $tr_1$ 的 $\texttt{A}$ 儿子 $2$ 号节点。

• 最后更新 $last$ 指针指向 $5$。

---

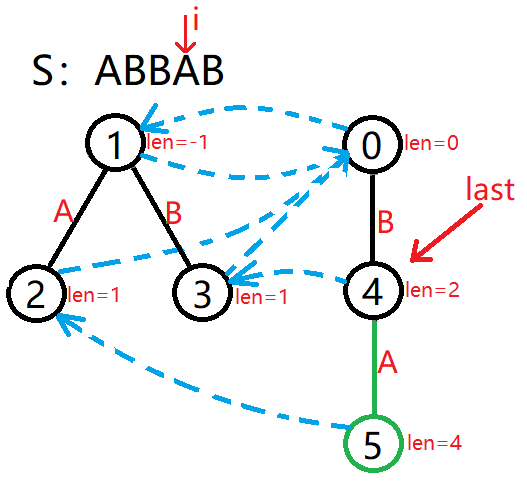
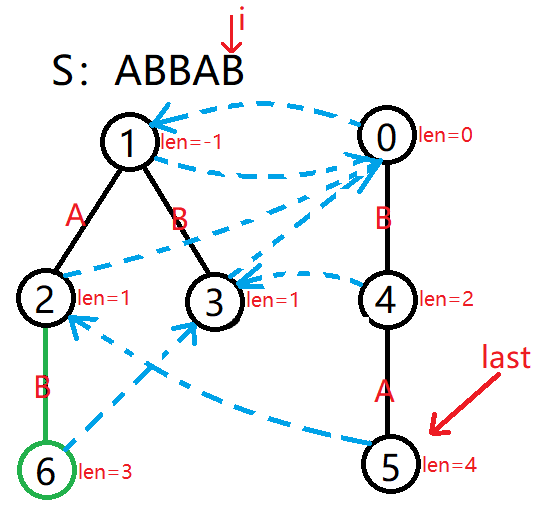
• 插入 $S=\texttt{ABBAB}$ 中的第 $5$ 个字符 $\texttt{B}$，那么我们已经建好了 $S$ 前 $4$ 个字符构成的回文树，并且此时 $last$ 指向 $5$。

• 此时 ${S_{i-len_5-1}=S_{5-4-1}=S_0=\varnothing \neq S_5=S_i}$，所以接着判断 $fail_5$ 指向的 $tr_2$。
  由于 ${S_{5-len_2-1}=S_{5-1-1}=S_3=\texttt{B}=S_5=S_i}$，所以在 $tr_2$ 下面新建一个 $\texttt{B}$ 节点（$tr_6$）即可，节点所对的回文串的 $len$ 值为 $1+2=3$。

• 进行此节点 $fail$ 指针的计算：$tr_6$ 的父亲节点是 $tr_2$，所以从 $fail_2$ 指向的 $tr_0$ 开始判断。
  此时 ${S_{5-len_0-1}=S_{5-0-1}=S_4=\texttt{A} \neq S_5=S_i}$，所以接着判断 $fail_0$ 指向的 $tr_1$。
  由于 ${S_{5-len_1-1}=S_{5-(-1)-1}=S_5=\texttt{B}=S_5=S_i}$，匹配成功，所以将 $fail_6$ 指向 $tr_1$ 的 $\texttt{B}$ 儿子 $3$ 号节点。

• 最后更新 $last$ 指针指向 $6$。

---

模板代码

在这里先给出 init 初始化函数和 insert 插入节点函数的代码。

string s;//原字符串 
int tot,last;
//tot的定义同字典树，last为 以上一个字符为结尾的最长回文子串 在回文树上所对应的节点编号 
struct TREE{
    int son[26];
    int len;//此节点所对应回文串的长度 
    int fail;//此节点所对应回文串的最长回文后缀 
} tr[N];
void init(){//初始化 
    tr[1].len=-1,tr[0].len=0;//tr[1],tr[0]的len分别为-1,0
    tr[1].fail=0,tr[0].fail=1;//tr[1],tr[0]的fail指针分别指向0,1 
    tot=1,last=1;//last初始化成1 
}
int getfail(int x,int i){//进行后缀链跳跃，找到以i-1结尾的最长的可以两边拓展的回文串 
    while(s[i-tr[x].len-1]!=s[i]){
        x=tr[x].fail;//继续判断x节点所对应回文串的最长回文后缀 
    }
    return x;
}
void insert(int x,int i){//插入节点 
    int fa=getfail(last,i);//找要接在哪个节点下面 
    int j=tr[fa].son[x];//j是当前节点 
    if(!j){//需要新建节点 
        j=++tot;
        tr[fa].son[x]=j;
        tr[j].len=tr[fa].len+2;//更新len 
        int tmp=getfail(tr[fa].fail,i);//找fail指针的父亲 
        if(fa!=1) tr[j].fail=tr[tmp].son[x];
    }
    last=j;//更新last 
}

---

常见应用

有关每个回文子串长度和出现次数

先对这个回文串建出回文树，回文串的长度在建回文树的时候已经求好了，所以关键是求每个回文子串的出现次数。

假设我们现在要求回文子串 $T$ 的出现次数。

由于回文树上存储的是以每个字符结尾的最长回文子串，所以我们可以把 $T$ 的出现次数分成两类：

1. $T$ 是以 $i$ 结尾的最长回文子串。

2. $T$ 是以 $i$ 结尾的回文子串，但不是最长的。

对于第一类，$T$ 的出现次数即为它在回文树上被统计的次数。

对于第二类，$T$ 的出现次数是「以 $T$ 为最长回文后缀的回文串」的出现次数之和，即所有 $fail$ 指针指向 $T$ 的回文串数量之和。

由于 $fail$ 指针总是指向下标比它小的节点，所以我们只需倒序枚举所有回文树节点，就能递推算出每个回文串的出现次数。

代码如下：

void insert(int x,int i){
    int fa=getfail(last,i);
    int j=tr[fa].son[x];
    if(!j){
        j=++tot;
        tr[fa].son[x]=j;
        tr[j].len=tr[fa].len+2; 
        int tmp=getfail(tr[fa].fail,i);
        if(fa!=1) tr[j].fail=tr[tmp].son[x];
    }
    tr[j].cnt++;//统计第一类出现次数 
    last=j;
}

for(int i=tot;i>=2;i--){
    tr[tr[i].fail].cnt+=tr[i].cnt;
}//统计第二类出现次数

---

例题：P3649 [APIO2014] 回文串

洛谷传送门

给定一个字符串，求：所有回文子串中，长度乘上出现次数的最大值。

解题思路

这题算是回文树的模板题了。直接对于所有不同回文串，求出其长度和出现次数，乘起来取最大就行了。

参考代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=300005;
string s;//原字符串 
int n;
int tot,last;
//tot的定义同字典树，last为 以上一个字符为结尾的最长回文子串 在回文树上所对应的节点编号 
struct TREE{
    int son[26];
    int len;//此节点所对应回文串的长度 
    int fail;//此节点所对应回文串的最长回文后缀 
    int cnt;//此节点所对应回文串的第一类出现次数 
} tr[N];
void init(){//初始化 
    tr[1].len=-1,tr[0].len=0;//tr[1],tr[0]的len分别为-1,1
    tr[1].fail=0,tr[0].fail=1;//tr[1],tr[0]的fail指针分别指向0,1 
    tot=1,last=1;//last初始化成1 
}
int getfail(int x,int i){//进行后缀链跳跃，找到以i-1结尾的最长的可以两边拓展的回文串 
    while(s[i-tr[x].len-1]!=s[i]){
        x=tr[x].fail;//继续判断x节点所对应回文串的最长回文后缀 
    }
    return x;
}
void insert(int x,int i){//插入节点 
    int fa=getfail(last,i);//找要接在哪个节点下面 
    int j=tr[fa].son[x];//j是当前节点 
    if(!j){//需要新建节点 
        j=++tot;
        tr[fa].son[x]=j;
        tr[j].len=tr[fa].len+2;//更新len 
        int tmp=getfail(tr[fa].fail,i);//找fail指针的父亲 
        if(fa!=1) tr[j].fail=tr[tmp].son[x];
    }
    tr[j].cnt++;//统计第一类出现次数 
    last=j;//更新last 
}
int main(){
    cin>>s;
    n=s.length(),s=" "+s;
    init();
    for(int i=1;i<=n;i++){
        insert(s[i]-'a',i);
    }
    for(int i=tot;i>=2;i--){
        tr[tr[i].fail].cnt+=tr[i].cnt;
    }//统计第二类出现次数
    ll ans=0;
    for(int i=2;i<=tot;i++){
        ans=max(ans,1ll*tr[i].len*tr[i].cnt);
    }//统计答案 
    printf("%lld\n",ans);
    return 0;
}